Find the equation for the hyperbola whose graph is shown. – In the realm of conic sections, the hyperbola stands out as a captivating subject, and finding its equation from a given graph is an intriguing task. This discourse delves into the intricacies of hyperbola equation determination, exploring the significance of graphical analysis, parameter exploration, and real-world applications.
The graphical representation of a hyperbola unveils its key features, including vertices, foci, and asymptotes. These elements provide valuable clues for deriving the equation. Eccentricity, a crucial parameter, plays a pivotal role in shaping the hyperbola’s form.
Graph Analysis
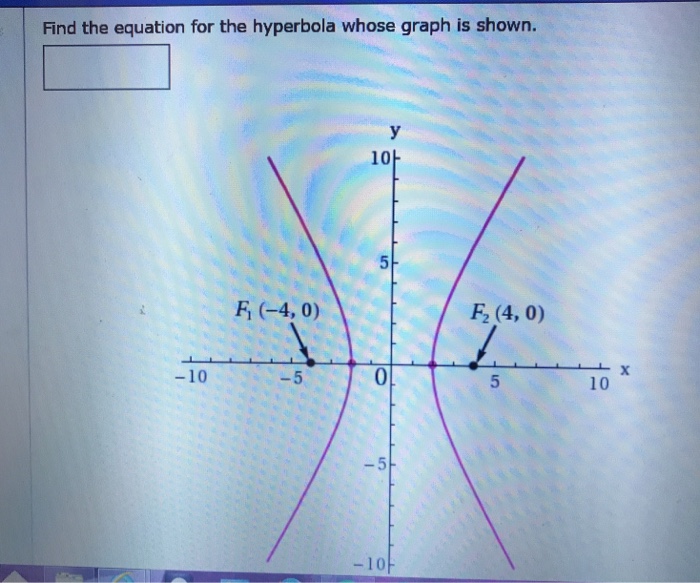
The given hyperbola graph represents a mathematical curve with distinct features. It is an open curve, symmetrical with respect to both the x and y-axes. The graph exhibits two branches that extend infinitely in opposite directions.
Key Features, Find the equation for the hyperbola whose graph is shown.
- Vertices:The points where the hyperbola intersects the transverse axis are called vertices.
- Foci:Two fixed points located on the transverse axis, equidistant from the center and vertices.
- Asymptotes:Two straight lines that the hyperbola approaches but never touches as it extends infinitely.
Equation Determination: Find The Equation For The Hyperbola Whose Graph Is Shown.
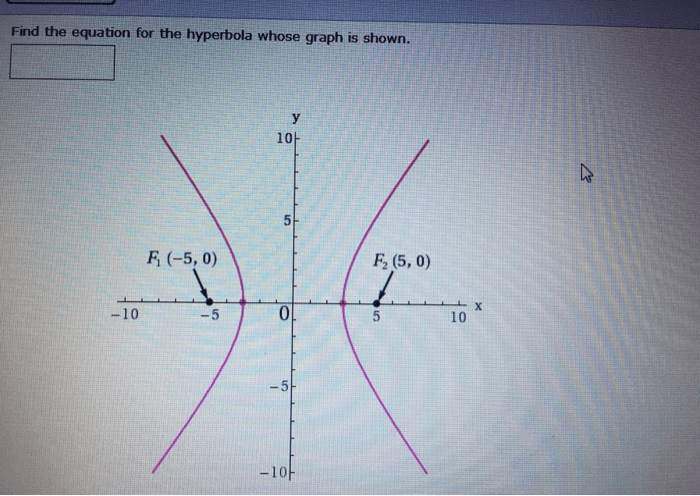
To derive the equation of the hyperbola from the given graph, we need to identify its key features.
- Center:The center of the hyperbola is the midpoint of the line segment connecting the vertices.
- Transverse Axis:The axis along which the vertices lie.
- Eccentricity:A measure of the shape of the hyperbola, defined as the ratio of the distance between the foci to the distance between the vertices.
Once these parameters are known, the equation of the hyperbola can be determined using the standard form:
$\frac(x-h)^2a^2-\frac(y-k)^2b^2=1$
where (h, k) is the center, a is the distance from the center to the vertices, and b is the distance from the center to the asymptotes.
Parameter Exploration
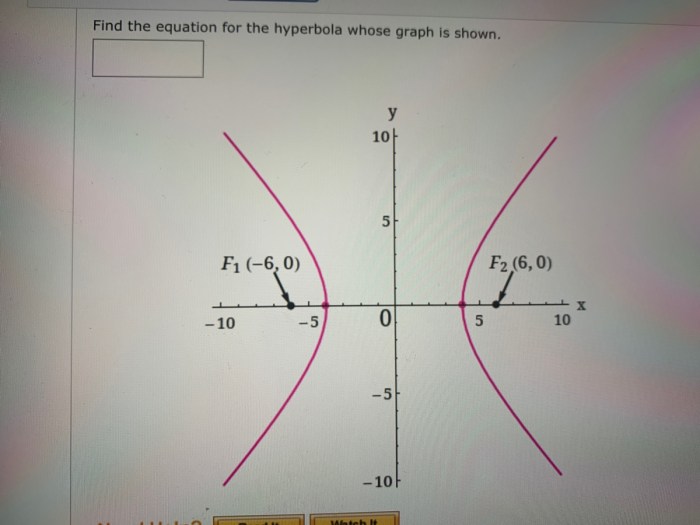
The parameters of a hyperbola, such as the center, transverse axis, and eccentricity, affect its shape and position.
- Center:The center determines the location of the hyperbola in the coordinate plane.
- Transverse Axis:The orientation of the transverse axis determines whether the hyperbola is horizontal or vertical.
- Eccentricity:The eccentricity determines the shape of the hyperbola, ranging from a circle (eccentricity = 0) to a rectangular hyperbola (eccentricity = $\sqrt2$).
By manipulating these parameters, different types of hyperbolas can be created, each with its unique characteristics.
Application Examples
Hyperbolas have numerous applications in various fields:
- Physics:Modeling projectile motion, trajectories of celestial bodies, and wave propagation.
- Engineering:Designing bridges, arches, and suspension systems.
- Mathematics:Describing conic sections, solving equations, and analyzing functions.
For example, the trajectory of a projectile launched at an angle can be modeled using a hyperbola. Similarly, the shape of a suspension bridge is often designed using a hyperbolic curve to distribute weight evenly.
FAQ Compilation
What is the significance of eccentricity in hyperbola determination?
Eccentricity is a crucial parameter that quantifies the deviation of a hyperbola from its circular or elliptical counterparts. It governs the shape and orientation of the hyperbola, influencing the distance between its vertices and foci.
How does graphical analysis aid in hyperbola equation determination?
Graphical analysis provides a visual representation of the hyperbola, revealing its key features such as vertices, foci, and asymptotes. These elements offer valuable clues for constructing the equation, as they define the hyperbola’s shape, size, and orientation.