Find an orthonormal basis of the plane . – In the realm of linear algebra, the concept of an orthonormal basis holds immense significance. It forms the cornerstone of many theoretical and practical applications. This article delves into the intricacies of finding an orthonormal basis of the plane, providing a comprehensive overview of its significance, methodology, and applications.
An orthonormal basis is a set of vectors that are mutually orthogonal (perpendicular) and have unit length. This unique property makes orthonormal bases invaluable for representing vectors in a coordinate system, simplifying calculations, and enhancing geometric understanding.
Orthonormal Basis of the Plane: Find An Orthonormal Basis Of The Plane .
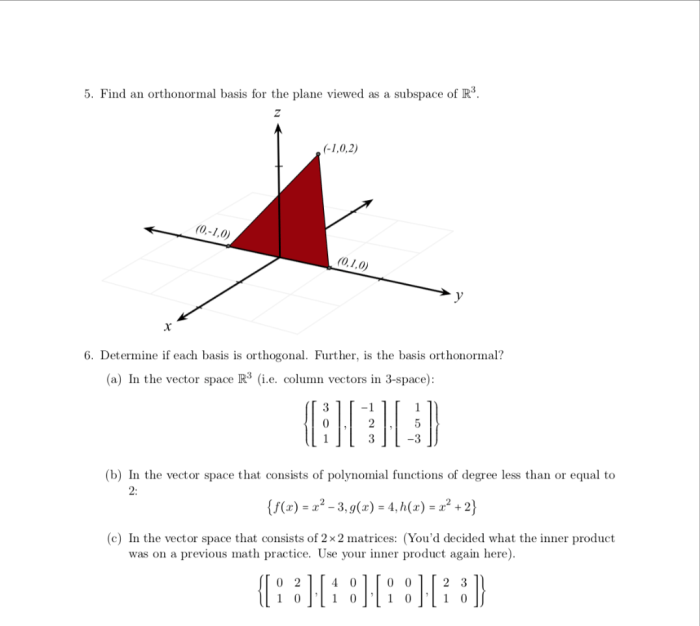
In linear algebra, an orthonormal basis of a vector space is a set of vectors that are mutually orthogonal and have unit length. Orthonormal bases are important because they provide a convenient way to represent vectors and perform calculations.
The problem of finding an orthonormal basis of the plane is a fundamental problem in linear algebra. In this article, we will discuss the Gram-Schmidt orthogonalization process, which is a method for constructing an orthonormal basis of any vector space.
Gram-Schmidt Orthogonalization, Find an orthonormal basis of the plane .
The Gram-Schmidt orthogonalization process is an iterative algorithm that takes a set of linearly independent vectors and constructs an orthonormal basis for the span of those vectors. The algorithm works as follows:
- Let v1be the first vector in the set.
- For each subsequent vector v i, subtract its projection onto the span of the previous vectors from v i.
- Normalize the resulting vector to obtain an orthonormal vector w i.
The set of vectors w 1, w 2, …, w nis an orthonormal basis for the span of the original set of vectors.
Geometric Interpretation
Orthonormal bases can be interpreted geometrically as vectors in the plane. The vectors are mutually orthogonal, which means that they are perpendicular to each other. The vectors also have unit length, which means that they have the same length as the unit vector.
The Gram-Schmidt orthogonalization process can be visualized geometrically as follows:
- Start with the first vector v1. This vector is represented by a line segment from the origin to the point (v 11, v 12).
- For each subsequent vector v i, find its projection onto the span of the previous vectors. This projection is represented by a line segment from the origin to the point (v i1, v i2).
- Subtract the projection from v ito obtain the vector w i. This vector is represented by a line segment from the point (v i1, v i2) to the point (w i1, w i2).
The set of vectors w 1, w 2, …, w nis an orthonormal basis for the plane.
Applications
Orthonormal bases are used in a variety of applications, including:
- Solving systems of equations
- Finding projections
- Performing linear transformations
Orthonormal bases simplify calculations and enhance understanding in these applications.
Frequently Asked Questions
What is the significance of orthonormal bases in linear algebra?
Orthonormal bases provide a convenient and efficient way to represent vectors in a coordinate system. They simplify calculations, enhance geometric understanding, and facilitate the solution of systems of equations.
How can I find an orthonormal basis of the plane using the Gram-Schmidt orthogonalization process?
The Gram-Schmidt orthogonalization process involves a series of steps to transform a set of linearly independent vectors into an orthonormal basis. It begins by normalizing the first vector, then subtracting its projection from the second vector, normalizing the result, and continuing this process for all vectors in the set.
What are some applications of orthonormal bases?
Orthonormal bases are widely used in various fields, including computer graphics, quantum mechanics, and signal processing. They are essential for solving systems of equations, finding projections, and representing vectors in a coordinate system.

